Determinantes de orden 3

Los determinantes son muy utilizados en las matemáticas. Nos permiten encontrar soluciones a sistemas de ecuaciones por mencionar alguna de sus aplicaciones. Detallaré como se calcula un determinante de orden tres y mencionaré las propiedades de los mismo.

Tambien hay métodos mas prácticos para resolver determinantes de orden superior, pero será tema de otro post.

Vamos al punto:

Sea V3 (K) un espacio vectorial de dimensión 3 sobre un cuerpo K, y una base B del mismo: B = ( u1 , u2 , u3 ). Y sean tres vectores de V3 u , v y w cuyas componentes en la base B son las siguientes:

 

 

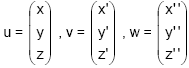
Se denomina determinante de la terna ( u, v, w ) a un escalar que puede calcularse como:

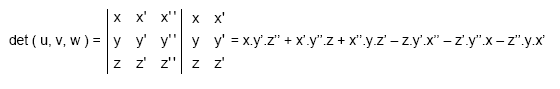
Este escalar, una vez que se fija una base, siempre se puede calcular y es único, esto nos permite definir una función «Determinante»:

det: V3 x V3 x V3 → K

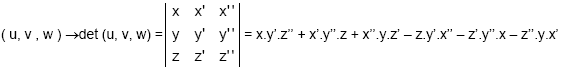
Esta función verifica las siguientes propiedades:

1) Es una forma trilineal:

Es decir que es lineal respecto a cada vector.

Que sea lineal respecto a u significa que:

– det ( u1 + u2 , v , w) = det ( u1 , v, w ) + det ( u2 , v , w ) siendo u = u1 + u2 para todo t de K

– det ( t.u, v, w ) = t. det ( u, v, w )

De manera análoga se expresa la linealidad respecto a v y a w.

2) Es una forma alternada:

( ∀ ( u, v, w ) ∈ V33 ) :

det (u, v, w) = det (v, w, u) = det (w, u, v) = – det (u, w, v) = – det (v, u, w) = – det (w, v, u)

3) El determinante se anula si se repiten vectores:

( ∀ ( u, v, w ) ∈ V33 ) :

det (u, u, v) = det (u, u, w) = det (u, v, v) = det (u, w, w) = det (v, w, w) = det ( v, v, w) = 0

Propiedades de los determinantes:

1. Si A y B son matrices cuadradas del mismo orden, entonces: det(A . B) = det(A) . det(B).
2. Si A es una matriz cuadrada y At es su traspuesta, entonces: det(A) = det (At).

3. Sea A una matriz inversible y A-1 su inversa, entonces: det(A) . det(A-1) = 1.

4. Sea A una matriz de orden n y t un escalar, entonces: det (t.A) = tn . det(A).

5. Si se permuta una fila por otra (o una columna por otra) el determinante cambia de signo.

6. Sea A una matriz cuadrada de orden n, si a una fila (o a una columna) se le suma un múltiplo de otra el determinante no varía.

7. El determinante de una matriz triangular es igual al producto de los elementos de la diagonal principal.

8. Sea A una matriz cuadrada, t un escalar y A’ la matriz que resulta de multiplicar una fila de A por el escalar t, entonces: det(A’) = t . det(A).

9. Si una matriz cuadrada tiene una fila o una columna completa de ceros, el determinante se anula.